Introduction. 1

A. Définition. 1

B. Historique. 2

B. 1. L'automate de John von Neumann. 2

B. 2. Le jeu de la vie. 3

B. 3. Les années 80 : L'ère Wolfram.. 3

B. 4. Actuellement 3

C. Cadre de l'étude menée. 5

C. 1. Les limites d'une approche purement statistique. 5

C. 2. Les automates binaires de rayon 1, en dimension 1. 5

C. 3. L'outil informatique (Partie I) 8

C. 4. Quelle mesure de complexité pour les ACL ? (Partie II) 8

C. 5. Quelles perspectives pour la notion de complexité ? (Partie III) 8

C. 5. Une indépendance relative. 8

 

Introduction

A. Définition

 

La qualification d'automate cellulaire caractérise un système dynamique doué de certaines propriétés générales dont la présentation fait l'objet de cette introduction. Il convient cependant de préciser que ces définitions n'entrent dans le cadre d'aucun formalisme "académique" et se sont simplement imposées de par leur simplicité.

 

q              Un automate cellulaire est un système dynamique totalement discret: dans le temps, dans l'espace et dans le nombre d'état atteints.

 

 

·        Discret dans le temps : on introduit le concept de génération, on peut la rapprocher de celle d'indice d'une suite. Matériellement, elle représente le temps de calcul d'un ordinateur qui fait évoluer l'automate. Cette donnée est donc considérée comme temporelle.

·        Discret dans l'espace : un automate est souvent représenté par un plage de cellules (ou cases) affectée de diverses valeurs.

·        Discret dans le nombre d'états atteints : l'ensemble des valeurs prises par une cellule est discret[1] (le plus souvent fini).

 

Ces caractéristiques rendent les automates particulièrement adapté au traitement informatique.

 

q              La seconde caractéristique fondamentale des automates cellulaires est que l'évolution d'une cellule donnée (dans l'espace) à la génération suivante (dans le temps) est entièrement déterminée par la donnée d'un voisinage de cette cellule. Le voisinage ne dépend pas de la cellule considérée.

 

L'évolution d'un automate est donc régie par une loi déterministe et homogène. La donnée des images de chacune des configurations possibles du voisinage par cette loi d'évolution, constitue la règle de l'automate cellulaire.

B. Historique

B. 1. L'automate de John von Neumann

 

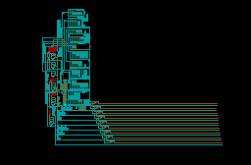
Les automates cellulaires ont été inventés par John von Neumann[2], en 1945. Celui-ci voulait résoudre le problème suivant: est il possible de créer un ordinateur (au sens de machine de Turing) qui puisse se reconstruire lui même? L'automate qu'il créa en est la preuve: il est de dimension deux (c'est à dire dans le plan), de voisinage carré de côté trois, et il peut atteindre 29 états suivant une règle complexe basée sur l'interaction entre la transmission d'impulsions et les temps de pauses induits par les cycles d'évolutions de bifurcateurs. Certaines cellules peuvent également en détruire d'autre. Cet automate permet de reconstituer des circuits intégrés virtuellement:

 

 

 

(ci-dessous): Structure simple de l'automate de Neumann

 

 

Structure ayant résolu le problème de Neumann (zoom --)	Structure codeuse (zoom --)

 

 

B. 2. Le jeu de la vie

 

Les automates tombèrent ensuite dans l'oubli jusque dans les années soixante-dix quand un chercheur du MIT, John Conway, créa un automate à deux dimensions, deux états et de voisinage carré de côté trois. Le jeu de la vie modélise de façon simplifiée les règles de survie d'une population biologique: Une cellule vivante (1) dans une zone isolée (moins de deux 1) ou surpeuplée (plus de trois 1) périra (>>0). Une cellule vide (0) entourée (de deux ou trois 1) sera remplie (>> 1).

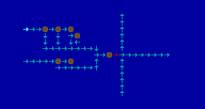
Des structures complexes peuvent apparaître (ou être crées ). On étudie surtout les vaissaux, structures qui se retrouvent identiques mais déplacés dans l'espace.

 

(ci-dessous): Glider (vaisseaux se déplaçant en diagonale de période 4)

 

 

Le jeu de la vie connut un vif succès et on découvrit un grand nombre de vaisseaux de toutes tailles et de toutes périodes, mais son intérêt pratique reste limité.

Dès lors l'étude des automates cellulaires s'orienta suivant trois voies:

·        Modélisation : On chercha à créer des règles représentant les lois régissants des phènomènes rattachés à divers domaine de la physique, de la biologie ou des sciences humaines (tels que la mécanique des fluides, l'agrégation, l'évolution de populations bactériologiques ou humaines, les phénomènes de files).

·        Etude intrinsèque : Quelques chercheurs essayèrent de mener une étude rigoureuse sur l'objet mathématique qu'est un automate cellulaire. Devant l'incommensurable complexité que génère une définition pourtant très simple, ils décidèrent de se limiter à des familles plus simples, essentiellement en dimension 1, avec des automates à états binaires (0 ou 1).

·        Informatique fondamentale : On continua à exploiter certains automates comme des objets informatiques, notamment en cryptographie.

B. 3. Les années 80 : L'ère Wolfram

 

            Au début des années 80 un mathématicien américain, Stephen Wolfram, présente une série de conférence sur des études essentiellement statistiques, mais également algébriques et linguistiques, sur le comportement de familles d'automates simples à une dimension. De façon empirique il distingue quatre familles d'automates cellulaires:

 

·      Classe I : Convergent vers une génération constante (automates convergents)

·      Classe II : Aboutit rapidement à un cycle simple

·      Classe III : Présente un comportement chaotique

·      Classe IV : Génère des structures complexes (supposé être des calculateurs universels)

 

Une recherche active se développe suivant de tels axes, notamment autour des universités américaines de Santa-Fe et du Massachusetts Institute of Technology.

A la fin des années 80, Wolfram abandonne la recherche pour développer et commercialiser le logiciel Mathematica. Au début des années 90, le développement d'Internet, très précoce dans cette communauté, permet une large diffusion des travaux inspirés de cette lignée[3].

B. 4. Actuellement

 

Mais ces types de descriptions montrent rapidement leurs limites (cf. C . Cadre de l'étude menée). La recherche "communautaire" s'essouffle et différentes voies sont suivies un peu partout dans le monde[4].

 

Par exemple: le projet Capow à Santa-Fe[5], le laboratoire d'informatique fondamentale de l'ENS Lyon[6], le projet Tierra de Tim Ray[7].

 

C. Cadre de l'étude menée

 

Les automates cellulaires présentent cette propriété particulière que des générations initiales simples peuvent générer une très grande complexité.

 

C. 1. Les limites d'une approche purement statistique

 

Comment quantifier la complexité? Dans les années 80, on développa des mesures statistiques basées sur les résultats de physique statistique telles que l'entropie (on considère les cellules binaires comme une distribution d'états).

Cependant cette mesure ne fait appel à aucun des caractères propres des automates cellulaires et si son évolution peut être signifiante pour qui connaît la thermodynamique, sa valeur exacte reste très obscure.

 

Nous avons décidé de partir des bases "wolframiennes" ( études exhaustives sur des familles d'automates cellulaires binaires de dimension 1), mais d'essayer de trouver un autre moyen de quantifier la complexité que la séparation empirique en quatre classes (ci-dessous).

 

·      Classe I : Convergent vers une génération constante

·      Classe II : Aboutit rapidement à un cycle simple

·      Classe III : Présente un comportement chaotique

·      Classe IV : Génère des structures complexes

 

On s'imagine la difficulté que représente une quantification non-triviale des expressions en gras.

 

C. 2. Les automates binaires de rayon 1, en dimension 1

 

q       Règle

 

La règle est une fonction de Z₂ ^Z dans lui même telle que la condition d'homogénéité soit vérifiée. La notion de règle est indépendante de la largeur de la génération, ou de la génération initiale.

On les nomme par un nombre décimal qui est l'équivalent du nombre binaire créé par les images accolées:

 

(ci-dessous) : Une règle de rayon 1 sous Autom

 

> rdisp

#   # Rule: 150   (10010110)

#   # 000-0    001-1    010-1    011-0

#   # 100-1    101-0    110-0    111-1

 

>

 

(ci-dessous) : L'équivalent de la règle précédente rayon 2 sous Autom

 

> rdisp

#   # Rule: 150   (10010110)

#   # 000-0    001-1    010-1    011-0

#   # 100-1    101-0    110-0    111-1

 

> rayset

Ray : 1 >> 2

 

> rdisp

#   # Rule: 49980   (11000011001111001100001100111100)

#   # 00000-0    00001-0    00010-1    00011-1

#   # 00100-1    00101-1    00110-0    00111-0

#   # 01000-1    01001-1    01010-0    01011-0

#   # 01100-0    01101-0    01110-1    01111-1

#   # 10000-0    10001-0    10010-1    10011-1

#   # 10100-1    10101-1    10110-0    10111-0

#   # 11000-1    11001-1    11010-0    11011-0

#   # 11100-0    11101-0    11110-1    11111-1

 

>

 

Par la suite, on assimilera la règle au nombre décimal qui définit son nom[8].

 

Une règle est dite inversible si quelque soit la largeur considérée il existe un et un seul antécédent par génération initiale :

 

 

(ci-dessous) : La règle identité sous Autom

 

> men

Rule          : 204   (11001100)

   Ray        : 1

Width         : 20

Nbr computed  : 6

Nbr displayed : 6

First gen.    : >g gggg   g gg   gg g<

 

> rdisp

#   # Rule: 204   (11001100)

#   # 000-0    001-0    010-1    011-1

#   # 100-0    101-0    110-1    111-1

 

> .run

 

 |>g gggg   g gg   gg g<| 0

 |>g gggg   g gg   gg g<| 1

 |>g gggg   g gg   gg g<| 2

 |>g gggg   g gg   gg g<| 3

 |>g gggg   g gg   gg g<| 4

 |>g gggg   g gg   gg g<| 5

 

q       Automate Cellulaire Libre (ACL)

 

Un ACL est la donnée d'une règle et d'un entier naturel L, la largeur de la génération sur lesquels la règle s'applique.

 

Cette notion de largeur revient en réalité à imposer une périodicité de L à l'ensemble des générations. Concrètement les cases les plus à gauche d'une bande de largeur L appartiennent au voisinage de celles les plus à droites.

Cette restriction rend l'automate calculable sans approximation par un ordinateur. On gardera à l'esprit qu'un automate cellulaire en tant qu'objet des mathématiques appliquées est un système dynamique "fini" dans ses dimensions.

 

On lui associe de façon naturelle l'ensemble

E_L =  { L-uplet de 0 et de 1 }

qui est l'ensemble des générations initiales de l'ACL.

On note que l'image de tout ACL et donc leur union est contenue dans E_L .

On définit la notion d'ACL inversible : c'est un ACL qui admet un et un seul antécédent par élément de E_L . Tout ACL de règle inversible est bien entendu inversible.

 

q       Automate Cellulaire Appliqué (ACA)

 

Un ACA est la donnée d'un ACL et d'un élément u de E_L . On lui associe de façon naturelle le graphe de la suite G_t de E_L telle que:

           

G₀    =  u

            G_t+1  =  ACL(G_t)

 

C'est l'image de l'ACA.

 

La notion d'ACA inversible sera précisée plus loin.

 

q       Bilan : Inclusions

 

Un ACL est la restriction d'une règle sur les générations périodiques de période L.

Un ACA est l'image d'un élément de E_L par un ACL.

 

C. 3. L'outil informatique (Partie I)

 

On a vu que l'étude des ACL et des ACA nécessitait l'utilisation de l'outil informatique. Cette exigence a été présente tout au long de l'étude. Les résultats que les programmes nous fournissaient permettaient de les améliorer au cours des versions successives.

Le choix du langage de programmation fut tout d'abord crucial. On verra comment nous essayâmes le C, le Java, puis le C⁺⁺. Nous présenterons l'évolution de la structure en fonction de celle de notre façon d'appréhender le problème.

 

Au terme d'un très long travail de construction des outils que nous jugions nécessaires, nous disposions d'une plate-forme stable sur laquelle nous pûmes greffer des outils de traitements statistiques. La partie II présente la partie la plus structurée de l'exploitation des  données fournies par ces outils.

 

C. 4. Quelle mesure de complexité pour les ACL ? (Partie II)

 

Cette partie de notre présentation présente une approche de la notion de complexité quantifiée à travers diverses mesures sur les cycles des ACL.

Les enjeux soulevés par ces notions ne sont apparut qu'au terme du travail de construction informatique et notre étude nous a fait déboucher sur des horizons qui pour en être attirants n'en sont pas moins lointains.

 

L'aspect nécessairement réducteur du choix d'axes d'étude privilégiés (complexité, cycles, inversibilité, …), rend nécessaire la présentation des axes que nous avons peu développés ou qui se situe dans le prolongement de cette étude et pour lesquels certaines notions sont déjà clarifiées. C'est l'objet de la partie III de notre présentation.

 

C. 5. Quelles perspectives pour la notion de complexité ? (Partie III)

 

Au cours de notre travail nous avons dû procéder à certains choix. Cependant avant de les effectuer nous avons été amener à exploiter certaines idées avant de les abandonner au profit d'une autre logique. Ces résultats invitent de par leur diversité même à se refuser toute tentative de formalisme absolu sur les automates cellulaires. Ils sont chacun présentés avec les limites qu'ils rencontrent et les perspectives qu'ils offrent.

 

C. 5. Une indépendance relative

 

Les différentes parties de cet exposé sont construites de façon indépendantes. Cependant leur ordre représente une prise de conscience progressive des formes que pouvait prendre la complexité que l'on devine intuitivement à la lecture de la représentation d'un automate.

Enfin, on trouvera en Annexes certains listings de données fondamentales et des précisions sur certains points qui ne constituent pas exactement le sujet de cette présentation.