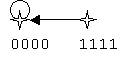A. Reflexions et point de vue autour des cycles. 1

A. 3. Segments et cercles. 3

A. 4. Régime transitoire et régime établi 7

B. Complexité d’un automate. 8

B. 1. Complexité mesurée par T et t. 8

B. 2. Présentation des résultats. 9

Nuages de points T(t), largeur de 4 à 10. 10

Représentation par bulle. 12

B. 3. Introduction de p et l. 13

C. Inversibilité. 15

C. 1. Cycles et inversibilités. 15

C. 2. L'automate 150. 16

C. 3. Résultats du détecteur d'inversibles. 19

II Cycles et complexité

A. Reflexions et point de vue autour des cycles

A. 1. Nomenclature

Nous avions dans un premier utilisé le terme générique d’automate cellulaire. Lors de notre étude, il nous est apparu que cette notion était trop vague et que nous manipulions des objets de nature très différente que nous avons tous, dans un premier temps, appelés automates cellulaires. Nous avons établi une nomenclature plus précise qui paraît adapté à notre étude. Une première vision de ces nouveaux objets a été donnée en introduction. Nous proposons ici une autre approche, totalement équivalente.

Le premier type d’objet et le plus général est la règle. Il s’agit de la donnée de 2.r + 1 paramètres, r étant le rayon, traduisant l’opération locale du passage d’une génération à la suivante. Pour chacun des environnements possibles d’une cellule à la génération n, la règle donne le résultat pour cette cellule à la génération n+1

Par exemple, une règle de rayon 1 particulière est :

000 Þ 0

001 Þ 1

010 Þ 1

011 Þ 0

100 Þ 1

101 Þ 0

110 Þ 0

111 Þ 1

Avec cette règle, à partir d’une génération initiale 10001110, on obtiendra la génération 11010101, en déplaçant sur la génération de départ un module de 3 cases donnant la valeur de la case du milieu pour la nouvelle génération.

Il existe règles pour un rayon r, soit 256 règles pour le rayon 1 auquel on s’intéresse plus particulièrement ici. Afin de simplifier les notations, il a été pris pour habitude de nommer les règles par l’équivalent décimal du nombre en base 2 qui caractérise la règle.

Ici, , donc la règle sera dénommer règle 150.

Le second type d’objet comprend deux informations : une règle et une largeur. Nous avons choisi de l’appeler automate cellulaire libre (ACL), par opposition à l’automate cellulaire appliqué (ACA), qui constitue le troisième type d’objet et qui est caractérisé, en plus d’une règle et d’une largeur, par une génération initiale.

L’automate cellulaire appliqué ne possède plus de degré de liberté. Toute génération n est entièrement déterminée et peut être calculée grâce à la règle. L’automate cellulaire libre s’applique à une génération de départ. C’est une fonction de l’ensemble des générations de départ, isomorphe à {0,1,...,- 1} avec L largeur, dans l’ensemble des ACA. L’intérêt d’un tel objet apparaît notamment dans le programme ainsi que dans notre étude de l’inversibilité des automates.

A. 2. Notion de cycles

Une grande partie de notre travail est fondé sur une réflexion à propos des cycles. On appelle cycle d’un automate cellulaire un ensemble de n générations successives telles que la n+1 ème serait égale à la première.

|>00 000 0 0 0 0 00 <| 0

|> + ++++ + + + +<| 1

|>+ ++++ ++ + ++ +++ ++<| 2

|> ++ ++ +++ + + + +<| 3

|> + + + + ++ ++ ++ +<| 4

|>+ +++++ + ++ + + + +<| 5

|> + + +++ + ++ ++++++ + <| 6

|>+++++ + ++++ + + + ++++ ++<| 7

|>++++ +++ ++ ++++++ + ++ ++ +<| 8

|>+++ + ++ ++++ +++ <| 9

|> + + ++ + + ++ ++ + + +<| 10

|> + + + +++++ + ++ ++<| 11

|> + ++ ++ +++ + ++ + + <| 12

|>++ ++ + ++ + + ++ ++ <| 13

|> + + +++ + +++++ <| 14

|> +++ +++ + + +++ +++ + <| 15

|>+ + ++ + + + + ++ + ++ <| 16

|>+ + ++++ ++++ +++ + +<| 17

|> ++ + ++ ++ + + + ++++ + <| 18

|> + +++ + + ++++ + ++ ++<| 19

|> +++ + + ++ ++ + ++ +++ ++ <| 2+

|>+ + + + + ++ + ++ + <| 21

|>+ ++++ ++ +++ + + +++ <| 22

|>+ ++ + + + ++ +++ + + <| 23

|>+++ + +++ ++ +++ + + +++<| 24

|>++ +++++ + + + +++++ ++<| 25

|>+ +++ ++ ++ +++ +++ ++ +<| 26

|> + + + ++ + + + + <| 27

|>++ + + +++++++ +++ +++ <| 28

|> + ++ + +++++ ++ + + + +<| 29

|>+ ++ + +++ ++ ++ ++ ++<| 30

|> 0 0000 0 0 0 0<| 31

|>0 0000 00 0 00 000 00<| 32

|> 00 00 000 0 0 0 0<| 33

|> 0 0 0 0 00 00 00 0<| 34

|>0 00000 0 00 0 0 0 0<| 35

|> 0 0 000 0 00 000000 0 <| 36

|>00000 0 0000 0 0 0 0000 00<| 37

|>0000 000 00 000000 0 00 00 0<| 38

|>000 0 00 0000 000 <| 39

|> 0 0 00 0 0 00 00 0 0 0<| 40

|> 0 0 0 00000 0 00 00<| 41

|> 0 00 00 000 0 00 0 0 <| 42

|>00 00 0 00 0 0 00 00 <| 43

|> 0 0 000 0 00000 <| 44

(Les cases "pleines" sont représentées par des + pendant le premier cycle)

Le résultat théorique fondamental de notre étude est que tout automate cellulaire appliqué parvient au bout d’un certain nombre de génération à un cycle. En effet, la largeur L étant donnée, il existe un nombre fini de lignes (ou de cercles puisque les automates que nous étudions sont « cylindriques ») par lesquelles l’automate peut passer, ce nombre valant . Au bout de + 1 générations, l’automate donnera donc une ligne par laquelle il est déjà passé, et puisque le processus qui permet de calculer une génération à partir de la précédente est totalement déterministe, il redonnera la même suite de génération que lors du premier passage.

A partir de ce théorème, nous avons construit une des premières fonctions de notre programme, la fonction .cyc, qui donne la taille et la composition des générations du cycle atteint par un automate cellulaire appliqué. Le fonctionnement est simple : l’ordinateur calcul la + 1 ème génération, la garde en mémoire et calcule les générations suivantes jusqu'à retrouver la même ligne.

Du point de vue des automates cellulaires libres, on peut dire que chacun d’eux possède un nombre fini p de cycles C1,..., Cp, correspondant à l’ensemble des cycles auquel les ACA dérivant de l’ACL peuvent mener. Il est possible - et fréquent - que plusieurs ACA mènent au même cycle. Ce résultat est systématique chez les ACL possédant un cycle de périmètre supérieur ou égal à 2, puisque toutes les lignes de ce cycle prises comme générations initiales mènent (instantanément) au cycle.

A. 3. Segments et cercles

Il convient d’insister sur l’importance de la nature « cylindrique » des automates que nous avons choisi d’étudier. Les automates pyramidaux, c’est à dire de largeur infinie et dont les générations sont remplies par une infinité de 0 à gauche et à droite de la zone intéressante, ne mènent pas nécessairement à des cycles.

Cette dimension circulaire des générations pose des problèmes importants. En effet, nous avons dit qu’il existait lignes possibles, considérant donc que 10000, 01000, 00100, 00010 et 00001 sont 5 lignes différentes (avec L=5) alors que les 1 et les 0 sont disposé sur un cercle sans origine et avec seulement une orientation. Les cinq cercles donnés devraient donc n’être qu’un seul et même cercle, avec 5 écriture linéarisées différentes.

Ce problème se pose effectivement pour les générations initiales. Il paraît peu adroit de considérer que les ACA possédant des conditions initiales identiques à une rotation près sont des automates différents, puisque seule la représentation linéarisée (qui est de loin la plus facile d’abords) de ces automates changera.

Pour les générations filles, la question est différentes. Les suites de générations 10000Þ01111, 10000Þ10111, 10000Þ11011, 10000Þ11101, 10000Þ11110 ne sont absolument pas équivalentes. En fait, la question de la représentation en ligne d’un cercle ne se pose qu’une fois, puisqu’à partir de celle du cercle initial on obtient un mode de passage du cylindre à un rectangle, valable donc quelle que soit la génération. Dans notre exemple, il faudrait choisir de représenter la ligne contenant un 1 et 4 0 d’une manière ou une autre, disons 10000, et les générations suivantes seraient transposées de la même manière (c’est à dire en ouvrant le cylindre suivant une verticale).

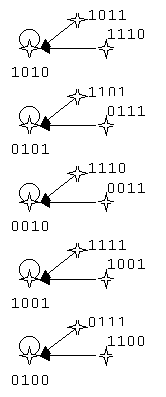
On peut parler de classes d’équivalence pour les représentation en ligne d’un même cercle. Par exemple, pour L=4, on a les classes d’équivalences {0000} et {1111}ne contenant qu’un élément, {1000}, {1100}, {1110} en contenant chacune 4, {1010} en contenant 2. Remarquons que les classes d’équivalence regroupent les générations appartenant à un même cycle des automates cellulaires libres 240 ou 170, qui à une ligne associe respectivement la même décalée à droite et à gauche.

La démarche que nous avons adopté pour mesurer certains critères de complexité d’un ACL est la moyenne sur chaque condition initiale de certains paramètres ayant trait aux cycles. Il fallait donc lancer les ACA correspondant à chacune des générations initiales. Il nous est apparu délicat de trouver un algorithme efficace (c’est à dire rapide, car pour chacun des ACA, le nombre d’opération à effectuer est supérieur à ) permettant de générer pour chaque largeur L l’ensemble des générations initiales « circulaires » (c’est à dire en ne générant qu’une seule ligne par classe d’équivalence).

A la fin de notre étude, nous étions capable de fabriquer un tel générateur. Nous savions en effet comment programmer une fonction rentrant dans un fichier ou un tableau une ligne de chaque cycle d’un ACL. En prenant les automates décalages (règles 240 ou 170), on obtient un représentant et un seul de toute classe d’équivalence pour la largeur L choisie. Il suffit ensuite que le programme effectuant les moyennes lise une à une les conditions initiales.

Signalons également que nous avons cherché un algorithme générant immédiatement ces générations initiales circulaires. Une de nos idées les plus exploitables reposait sur la notion de période dans une ligne. Une ligne composée uniquement de 0 ou de 1 possède une période de 1 (module de taille 1 répété L fois), une ligne contenant un 1 et que des 0 a une période de L. Lorsque l’on parle de période, on entend période minimale, étant bien entendu que si L est pair, une ligne ne contenant que des 0 peut également être décrite comme la répétition de L/2 fois le module [00].

Une ligne de période 1 est de toute évidence seule dans sa classe d’équivalence, alors qu’une ligne de période L est dans une classe d’équivalence contenant L-1 autres éléments. De plus, une ligne peut avoir une période de taille P si et seulement si P divise L. L’idée était de générer les conditions initiales périodes par périodes. Mais la difficulté était de ne pas générer les lignes de périodes A lorsque l’on travaillait sur les périodes A.B. nous n’avons pas trouvé de caractérisation de la minimalité d’une période assez simple et assez rapide pour être exploitée en informatique.

Nous avons finalement décidé de générer générations initiales, en ayant bien conscience que cela signifiait créer L fois la ligne 100...0 et une seule fois la ligne 0...0. Ceci allait donc introduire des pondérations non désirées dans les calculs des moyennes effectuées sur les conditions initiales. Ce choix était motivé par la simplicité du générateur de lignes et sa rapidité, ainsi que par la facilité, avec cette convention, à représenter une « carte » d’un ACL. En effet, nous voulions parvenir à des diagrammes constitué de points représentant chacune des lignes ainsi que de flèches symbolisant les transitions possibles. Pour cela, il est impossible de choisir deux objets différents : les classes d’équivalences pour les générations initiales, les lignes pour les générations filles. Chaque génération ne devait en effet n’apparaître qu’une fois et pouvoir être une génération initiale d’un ACA dérivant ainsi qu’éventuellement une étape d’un ACA ayant une autre génération initiale.

exemple pour l'ACL (150, L=6)

Règle 76, L=5

Les résultats statistiques obtenus par moyenne sur les génération initiales circulaires et linéaires ne sont pas identiques, car on a vu que la moyenne "linéaire" correspondait à une moyenne "circulaire avec pondération en fonction de la période de la génération.

A partir de cette réflexion sur la différence entre générations linéaires et circulaires, nous avons également dégagé la notion de sous - cycle. Il est fréquent qu’un automate donne à la génération n+k la même ligne qu’à la génération n avec un décalage, donc une génération appartenant à la même classe d’équivalence.

Comme lors notre recherche sur les périodes, nous sommes arrivés à des considérations arithmétiques. En effet, si l’on arrive après un sous cycle de k générations à un décalage de D compté vers la droite, on arrivera au cycle après répétition de p sous cycles, avec

D.p = L.q

où p et q sont premiers entre eux (sinon on obtient également un cycle, mais qui n’est pas le cycle minimal)

on a donc p divisant L et q divisant D

d’où L = r.p et D = r.q

avec r = pgcd ( L, D)

Le cycle comporte un maximum de sous-cycles si L et D sont premiers entre eux (p=L).

A. 4. Régime transitoire et régime établi

Pour tout ACA, on peut définir deux phases : celle pendant laquelle il est sur un chemin menant à un cycle, et celle pendant laquelle il est sur le cycle. Par analogie avec des phénomènes physiques et notamment électrocinétiques, nous avons choisi d’appeler régime transitoire la première phase et régime établi la seconde. Il est possible que le régime établi arrive directement, c’est à dire que la génération initiale appartienne à un cycle. C’est une situation particulièrement intéressante comme on le verra plus tard. La première génération appartenant au cycle vers lequel se dirige l’ACA sera appelée génération critique.

La durée du régime transitoire nous a paru être une donnée intéressante. Nous l’avons nommée t. L’autre valeur significative est la période du cycle, notée T. Chacun des concepts caractérise une des phases de l’ACA. L’une ou l’autre des valeurs est intéressantes en fonction du type d’étude que l’on souhaite mener sur l’automate.

Nous nous étions fixés comme objectif de trouver certaines informations sur la complexité d’un automate. Après avoir établi cette interprétation physique de l’automate, nous avons décider d’utiliser ces deux notions (t et T) comme indicateur de complexité.

B. Complexité d’un automate

B. 1. Complexité mesurée par T et t

Un automate est intuitivement complexe du point de vue transitoire si le chemin vers le cycle est long.

Un automate est complexe en régime établi si la durée du cycle est importante. En effet, plus cette durée est grande, plus le nombre de données suffisant à caractériser le « mouvement » de l’automate sans utiliser la règle (c’est à dire la donnée de toutes les générations du cycle) est grand, donc plus il est complexe.

Obtenu avec la règle 173, la largeur 9,
la génération initiale 110000000, par la fonction .cyc

|> _ __ __ <| 0

|> ___ __ <| 1

|> __ __ _<| 2

|>__ __ _<| 3

|>_ __ _ _<| 4

|> __ ___<| 5

|>__ _ __ <| 6

|>_ ___ _<| 7

|> _ __ __<| 8

|> ___ __ <| 9

|>_ __ __ <| 10

|>___ __ <| 11

|>__ __ _ <| 12

|>_ __ __<| 13

|> __ _ __<| 14

|>__ ___ <| 15

|>_ _ __ _<| 16

|> ___ __<| 17

Length of the cycle: 18

Begin after 3 generations.

Obtenu avec la règle 161, la largeur 9,
la génération initiale 111101111, toujours pas la fonction .cyc

|>___ ___<| 0

|>__ _ __<| 1

|>_ _<| 2

|> _____ <| 3

|>_ ___ _<| 4

|> _ <| 5

Length of the cycle: 6

Begin after 7 generations.

Pour caractériser la complexité d’un ACL, nous avons choisi d’effectuer une moyenne de T et de t sur tous les ACA, c’est à dire les valeurs possibles de la fonction ACL. La mesure a l’avantage d’être simple à programmer et surtout rapide. Afin d’avoir des informations plus précises, le programme a été amélioré et permet d’obtenir les valeurs de T et de t pour chacune des conditions initiales, ces données étant injectées dans un fichier qui peut ensuite être exploité par un tableur (Excel pour nous). On peut ainsi disposer non seulement de la moyenne, mais aussi de l’écart type et des différents moments. Il est également intéressant de s’intéresser aux minima et aux maxima.

B. 2. Présentation des résultats

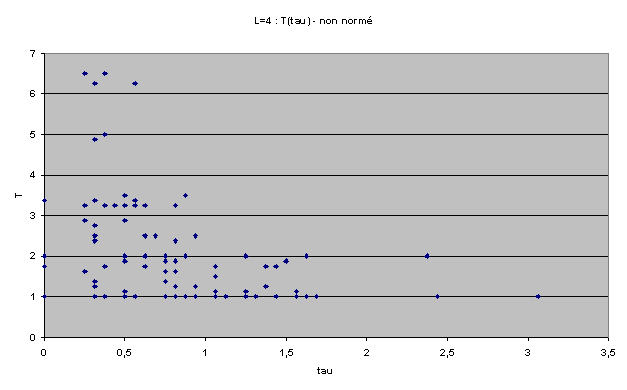
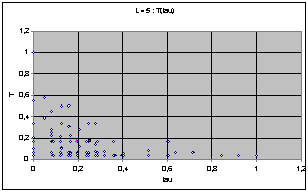
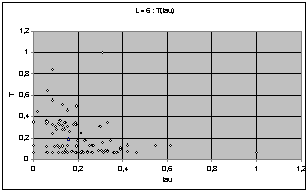
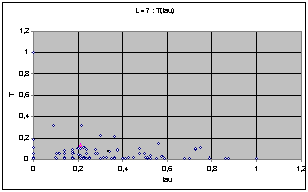
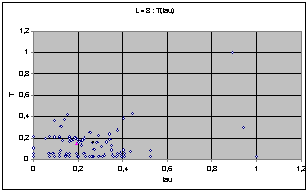
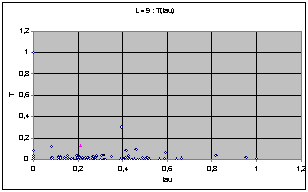
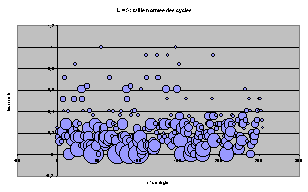
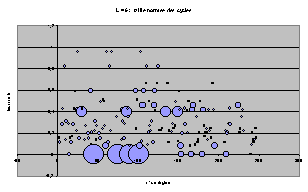
Nous avons d'abord cherché à exprimer T et t sur le même graphe afin de trouver une éventuelle répartition particulière. Pour une largeur donnée, on représente chacune des 256 règles de rayon 1 par un point ayant pour coordonnées les valeurs t et T de la règle. Voici le résultat obtenu pour L=4.

Pour L=4 on observe un nuage de points compris entre les deux axes et une hyperbole d'axes x et y. Voyant que les répartitions étaient très différentes d'une largeur à une autre, nous avons normés ces résultats en fonction du T et du t maximums pour chaque largeur.

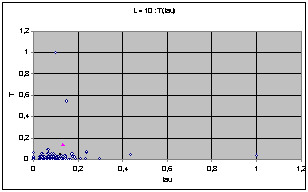
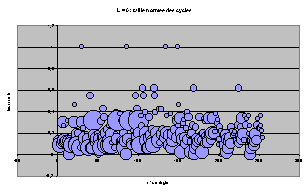
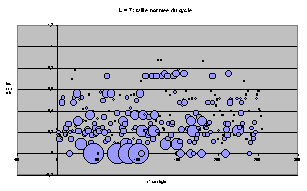
On obtient les diagrammes présentés ci dessous. Globalement, on observe un écrasement progressif du nuage quand L augmente. Cet écrasement se fait dans un premier temps parallèlement à l'axe des T, et à partir de la génération 9 suivant celui des t.

Puisque les graphes montrent des valeurs normées par le maximum, l'écrasement correspond en fait à l'apparition de cycles de très grande taille avec l'augmentation de L.

On perçoit une mutation de la forme du nuage de point qui semble chaotique. Les graphes peuvent laisser supposer que chaque largeur possède une structure profonde qui évolue de manière pour l'instant imprévisible (cf. Conclusion).

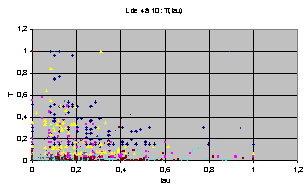
Nuages de points T(t), largeur de 4 à 10

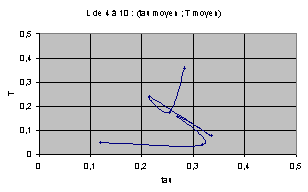
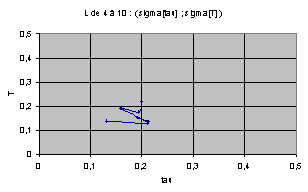
Dans l'optique de s'intéresser aux structures cachées des largeurs, nous avons réalisé des graphes montrant le déplacement avec la largeur du barycentre du nuage, c'est à dire un point ayant pour coordonnées les moyennes par largeur sur les règles de T et de t. Nous faisons remarquer que les échelles ont été multipliées par 2 entre les graphes précédents et ceux-ci.

Nous avons également représenté sur le graphe de droite la trajectoire d'un point de coordonnées les écarts types en T et en t.

Le premier graphe est surprenant. Tous les points moyennes semblent pouvoir être rattachés à une droite, l'une reliant 4, 6 et 10, l'autre 5, 7, 8 et 9 (4 est le point en haut à droite). Nous ne tirons pour l'instant aucun conclusion. On conjecture simplement que pour les grandes largeurs, la normation par les T et t maximaux fera converger la suite vers (0,0).

Le second graphe traduit la faible dépendance des écarts types avec la largeur. Ils restent entre 10 et 20 %.

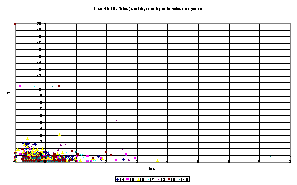
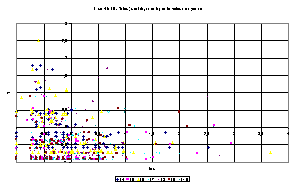
Pour éviter l'effet normation par le maximum, nous avons normé non plus par les valeurs maximales, mais par les moyennes, par largeur, de T et de t. Voici les graphes obtenus toutes largeurs confondues (vue d'ensemble et zoom) :

Avec une visualisation en couleurs, on constate qu'il n'y a pas de changement majeurs d'une distribution à l'autre lorsqu'on fait varier la largeur.

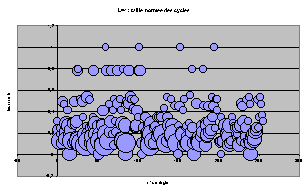
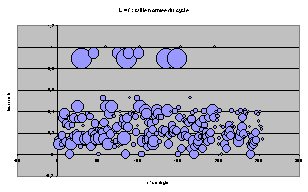
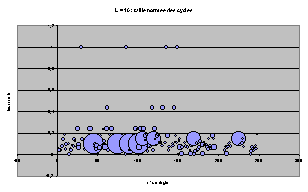
Représentation par bulle

Pour toutes les règles, classées par leur nom décimal suivant l'axe x, on représente l'ACL par un cercle de rayon proportionnel à T et placé à l'ordonnée t.

On retrouve les même tendances d'écrasement progressif et les structures particulières à chaque largeur.

On peut remarquer, maintenant que les règles sont étalées, qu'il existe beaucoup de groupes de 4 ACL de mêmes T et t, qui étaient superposés sur les graphes précédents. Il n'est pas très étonnant que cette structure par 4 revienne plusieurs fois.

En effet, il y a deux paramètres d'une règle que l'on peut modifier sans changer la nature profonde de la règle :

- la matérialisation du contenu des cellules par des 0 et des 1

- l'orientation droite - gauche.

Donc une règle est équivalente à celle obtenue en changeant tous les 0 en 1 et les 1 en 0 dans l'énoncé de la règle (y compris dans la colonne de gauche).

000Þ1 devient 111Þ0

001Þ0 devient 110Þ1 …

Une règle est également équivalente à la même où on inverse droite et gauche.

001Þ0 devient 100Þ 0

110Þ1 devient 011Þ1 …

D'où l'existence de classes de quatre ACL (parfois dégénérées en deux ou un si les règles sont leurs propres images par les transformations énoncées).

B. 3. Introduction de p et l

Bien sûr, il ne s’agit pas des seuls instruments de mesure de complexité. Pour le régime transitoire, il serait intéressant de connaître la longueur cumulée des chemins menant aux cycles. L’instrument que nous avons exploité, t, est une moyenne sur les conditions initiales, et donne donc une information assez différente. Si on a un chemin de longueur d, sa part dans t sera :

d +(d-1) + (d-2) + ... + 1 = d.(d+1)/2

donc une fonction en d², alors que sa part dans l, taille cumulée des chemins (qui est en fait un temps) sera strictement de d. Les chemins importants font grandir t beaucoup plus vite que l.

Pour le régime établi, on peut s’intéresser au nombre de cycle d’un ACL, ou, en suivant une démarche très analogue à celle qui mène de t à l, on peut définir p, somme des périmètres des cycles de l’ACL. Notons que si l’on pondère chacun des périmètres par le nombre de générations initiales qui mènent à ce cycle, on retrouve T multiplié par .

Il peut ensuite être intéressante de normer l et p en les divisant par (on obtient respectivement l' et p'). On pourra ainsi étudier leur évolution en faisant varier L, et essayer de définir une complexité propre à une règle. Notons la propriété l' + p' = 1. La « complexité totale » d’un ACL, vue sous cette perspective, est une constante. Ce qu’il est intéressant de rechercher, c’est la répartition de cette complexité entre complexité transitoire et complexité permanente.

Si on cherche à représenter sur un graphique p'(l') de la même manière que l'on représentait T(t) pour une largeur donnée, on obtient des points qui sont tous sur la droite

y = 1 - x. On peut alors mieux comprendre la forme particulière des diagrammes T(t) présentés précédemment. Ils correspondent à une déformation de la droite à cause de la pondération due aux mesures statistiques.

Nous n’avons pas utilisé ces mesures. Elles sont plus difficiles à mettre en place, car il est nécessaire de repérer les cycles ou les chemins et de ne compter qu’une fois chaque génération. Nous avons réfléchi au fonctionnement global de l’algorithme : le programme balayerait toutes les conditions initiales et chercherait le cycle atteint. A chaque cycle atteint, une génération de ce cycle est rentré en mémoire ainsi que la taille du cycle. Et avant de rentrer toute génération caractéristique d’un cycle en mémoire, on vérifierait que le cycle ne contient aucune des lignes caractéristiques précédemment enregistrées. On s’assure ainsi que tout cycle n’est compté qu’une seule fois. Le programme permet d’obtenir p. l est obtenu en soustrayant p à ou à 1 suivant que l’on est à faire aux variables normées ou pas.

Après avoir mis en place les instruments de mesure t et T pour les ACL, il est tentant d’utiliser la même démarche statistique pour mesurer « les complexités » d’une largeur L en faisant la moyenne sur les règles des automates cellulaires. On peut également s’interroger sur la complexité d’un rayon, voire sur la complexité d’une règle (en « normant » les mesures sur les ACL et en faisant une moyenne, si c’est possible, sur L).

C. Inversibilité

C. 1. Cycles et inversibilités

Une catégorie particulièrement intéressante d’automate est celle des inversibles. Il s’agit des automates pour lesquels il existe une et une seule génération antécédent pour chaque génération donnée.

On peut définir des notions d’injectivité et de surjectivité dans le cadre des automates cellulaires. Est injectif un automate tel qu’aucune génération n’est deux antécédents ou plus. Est surjectif un automate cellulaire tel que toute génération ait au moins un antécédent. Comme l’espace des lignes est fini, la surjectivité équivaut à l’inversibilité et à la bijectivité, c’est à dire à l’inversibilité.

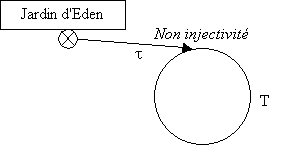
On introduit la notion de Jardin d'Eden (le nom ne vient pas de nous). Un Jardin d'Eden est une génération qui n'a aucun antécédent.

Non surjectivité

On peut donner une caractérisation visuelle de ce qu’est un automate inversible : il s’agit d’un automate ne possédant aucun embranchement (pour l’injectivité), c’est à dire aucun Jardin d’Eden (pour la surjectivité). A partir de cette remarque, nous avons imaginé un détecteur d’inversibilité d’ACL. Un ACL inversible est un automate formé uniquement de cycles disjoints, sans chemins menant aux cycles, donc un ACL dont tous les ACA dérivant ont un t nul, c’est à dire un ACL avec t = 0.

Il nous suffisait de greffer à notre calculateur de t et T un module reconnaissant les valeurs nulles de t et de créer un système de balayage des ACL.

Il est intéressant de noter que nous avions tous les deux des idées très différentes sur l’inversibilité. L’un pensait que l’inversibilité concernait les règles : si une règle est inversible lorsqu’elle est appliquée à une largeur L, elle est inversible pour toute largeur L. L’autre supposait plutôt qu’il fallait parler d’inversibilité d’ACL, notamment parce que des règles non inversibles pour des largeur classiques pouvaient le devenir avec une largeur inférieure au diamètre (d = 2.r +1 avec r rayon de la règle).

Par exemple :

> rset

No >>128

# # Rule: 128 (10000000)

# # 000-0 001-0 010-0 011-0

# # 100-0 101-0 110-0 111-1

n’est jamais inversible pour une largeur supérieure au diamètre, mais le devient avec une largeur de 1. En effet, les seules information de la règles qui sont utilisées sont 000 Þ 0 et 111 Þ 1, inversible évident. Il s’agit toute fois d’un cas très particulier, qui ne nous paraissait pas être un argument suffisant.

C. 2. L'automate 150

La question de l’inversibilité des règles ou des ACL a été tranchée avec l’étude « à la main » de la règle 150. Cette règle nous a servi de test régulièrement au cours de l’élaboration du programme en raison de la relative complexité des séquences de générations qu’elle donne. De plus, la règle peut s’écrire très aisément sous forme d’une fonction locale. Si x, y et z sont les trois cases de la génération mère, y’, case de la génération fille s’écrit :

y’ = x + y + z (addition binaire)

On peut donner la règle de l’automate 150 :

> rset

No >>150

# # Rule: 150 (10010110)

# # 000-0 001-1 010-1 011-0

# # 100-1 101-0 110-0 111-1

Le premier test de notre détecteur d’inversibilité nous a indiqué que l’ACL (règle=150, L=7) inversible. Un deuxième test avec L=8 a donné le même résultat. Nous avons commencé à nous intéresser à un générateur d’inverse, et pour cela, nous avons travaillé sur l’exemple de l’automate 150.

Nous avons trouvé un algorithme permettant de trouver à partir d’une génération donné la génération antécédente. Cet algorithme est propre à la règle 150 et ne peut pas être transposé pour n’importe quelle règle. Nous allons exposer son fonctionnement.

Pour chacune des case de la génération fille, la présence d’un 1 indique que dans les trois cases correspondantes de la génération mère se trouvent un nombre impaire de 1, la présence d’un 0 signifie un nombre paire de 1. La difficulté est de recouper les informations pour retrouver toute la ligne. Pour cela, nous avons eu l’idée de tracer une ligne simple au dessus de trois cases contenant un nombre impaire de 1, une double ligne au dessus de trois cases contenant un nombre paire de 1.

Ensuite, on fait l’hypothèse que le premier chiffre de la génération fille est un 0. La représentation avec les lignes permet de trouver le chiffre que contiendrait la quatrième case si la première contient effectivement un 0. En effet, si on regarde deux traits qui se suivent, les cases n et n+3 doivent remplir certaines conditions de parité. Deux traits identiques signifient que les deux cases doivent être remplies avec les même nombre, pour que les deux modules de 3 cases aient la même parité en nombre de 1. Si les traits sont différents, il faut que la case n+3 soit remplie avec ã=1-a si a est le contenu de la case n.

Avec ce processus, on peut peu à peu remplir les cases de la génération mère. Une fois le remplissage terminé, on vérifie que la génération mère engendre bien la génération fille, et si ce n’est pas le cas, c’est que l’hypothèse du 0 initial est fausse. On change alors tous les chiffres de la génération mère.







1	0	0	1	0	1	0	1	0	0	1	0	1	0	1	0	0	1	0	1	0
	0			1				0	0		1	1			0	0	1	1	1
															1	1	0	0	0

L’algorithme a bien fonctionné aux premiers essais. Mais lorsque l’on a essayé l’algorithme pour une largeur de 6, on est arrivé à une incohérence. Comme 6 est un multiple de 3, on retombe sur la première avant d’être passé par toutes les autres cases.








1	0	0	1	0	1	1	0
	0			1

Ici, le 1 de la quatrième case indique (2 traits simples) qu’il doit y avoir un 1 dans la septième case c’est à dire la première. Or celle-ci contient un 0.

Nous avons testé l’ACL(150,6) avec le programme, et nous avons trouvé qu’il était non inversible. De même pour L=9 et L=12.

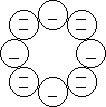
Il est possible de "démontrer" que pour toutes largeurs non multiple de 3, l’ACL(150,L) est inversible. En effet, l’algorithme d’inversion passe par toutes les cases avant de retourner à la première (3 et L sont premiers entre eux), et redonne nécessairement la même valeur que celle que l’on a fixé au début. Si on agglomère les traits successifs de même nature (par lesquels le passage n'entraîne aucun changement), on obtient le diagrame :

On voit que le cycle est formé par la répétition du module (-)(=), donc qu'il y a un nombre pair de transformations, et donc que l'effet final est nul. On n'aura jamais de contradictions.

De plus, parmi les deux générations possibles (images réciproques par la règle 51 de rayon 0 qui change chaque donnée - 1 devient 0 et 0 devient 1), une seule est un antécédent éventuel, puisque les deux lignes donnent par la règle 150 des lignes qui sont elles mêmes images réciproques par la règle 51.

Il apparaît donc une phénomène de période de non-inversibilité pour une règle. Cette période est ici de 3.

C. 3. Résultats du détecteur d'inversibles

Nous avons cherché tous les inversibles de rayon 1 pour des largeurs variant entre 4 et 10. Voici les résultats obtenus.

Règle

101

105

150

154

166

170

180

204

210

240

L=4

inv

L=5

inv

L=6

inv

L=7

inv

L=8

inv

L=9

inv

L=10

inv

On remarque la symétrie du tableau qui est due au fait que la transformation de tout 1 en 0 ne change rien à la nature intrinsèque de l’automate.

On peut définir deux types d’objets inversibles : Les règles et les ACL. Une règle est inversible si tous les ACL qui en dérivent sont inversibles. On distingue dans le tableau :

- les règles inversibles : 15, 51, 85, 170, 204, 240.

- les ACL inversibles dérivant de règles non inversibles : 45, 75, 89, 101, 105, 150, 166, 180, 210

Il est facile d’identifier les 6 règles inversibles et de démontrer qu’elles le sont bien indépendamment de la largeur. La règle 204 est l’identité, le 51 la transposition systématique, 170 et 240 sont les décalages sur la gauche et sur la droite, 85 et 15 les décalages sur la gauche et la droite suivis d’une transposition. Remarquons que ces 6 règles ne sont pas véritablement de rayon 1. En fait, la règle ne regarde à chaque fois qu’un seul des chiffres de la génération précédente, celui-ci n’étant pas nécessairement « au centre ». Nous appellerons ces règles des règles de poids 1. Dans le cas général, une règle de rayon un, donc de diamètre 3, est de poids 3 (le poids d’une règle est le nombre de cases de la génération mère qui ont effectivement une importance dans le calcul local de la génération fille).

Nous pouvons donc dire que seuls les règles de poids un sont susceptibles d’être inversibles (dans le cadre des règles de rayon 1. Le résultat est probablement généralisable aux rayons supérieurs).

Parmi les ACL inversibles dérivant de règles non inversibles, on remarque deux classes : ceux qui sont inversibles 2 fois sur trois (le 150 et le 105 qui est la composition du 105 avec le 51, la règle « vidéo inverse », VI) et ceux qui le sont une fois sur deux. Nous ne nous sommes pas intéressés dans cette étude à cette dernière catégorie, qui semblent cependant avoir des propriétés intéressantes.

On remarque également que les largeurs donnant le plus d’ACL inversibles correspondent aux nombres premiers (5 et 7). L’exemple du 150 peut aider à comprendre ce phénomène. Chaque diviseur de la largeur peut mener chez certains automates sensibles à des « blocage de l’inversibilité ».

Enfin, il faudrait s’intéresser aux règles de rayons supérieurs (jusqu'à r=E(L/2)) afin de compléter la liste d’automates inversibles.

Parmi les propriétés que nous avons observées sans les avoirs démontrés, citons le fait que toute règle inversible ou partiellement inversible (dont au moins un ACL dérivant est inversible) est sous forme binaire composée d'autant de 0 que de 1. On imagine bien qu'un nombre différent de réponses 1 et 0 entraînerait un déséquilibre et une perte de l'information incompatible avec un automate inversible.

La réciproque serait également intéressante : est-ce que toute règle "équilibrée en 0 et en 1" donne pour au moins une largeur L un ACL inversible ? Nous avons peu d'informations permettant de poser une hypothèse à ce sujet à cause des grands temps de calcul des tests d'inversibilité pour L supérieur à 10.

Les règles et ACL inversibles sont intéressants pour des applications en cryptographie. Il est en effet possible de coder une ligne binaire en transmettant séparément la n ème génération obtenue par un automate inversible, le nombre n ainsi que la règle de l'automate inverse.

Les inversibles les plus performants pour ce type de codage seraient ceux qui possèdent un seul cycle (Automates Cellulaires Libres Inversibles Suprêmes). On a ainsi le plus grand "éloignement" possible entre génération non codée et codée (il y a moins de chance pour que n soit supérieur à la taille du cycle) - mais nous ne sommes pas sûrs de leur existence. De plus, pour être sûr que la ligne codée est différente de la ligne non codée, il faut que la taille du cycle ne divise pas n. Donc si on prend n premier, cette condition est remplie quelle que soit la taille du cycle sur lequel se trouve la ligne non codée.